3PBDH

Étude sur les échanges de clés multipartites Diffie-Hellman

Attention : cette page contient des formules en LaTeX qui ne sont pas correctement supportées sur le site web, pour une meilleure expérience veuillez consultez la page sur Github.

Sommaire

3PBDH

Problématique

La cryptographie asymétrique permet d’assurer la confidentialité et l’authenticité des échanges entre deux ou plusieurs partis. Pour cela, chaque utilisateur possède une clé publique qu’il peut divulguer publiquement et une clé privée grâce à laquelle il assure être l’origine des messages qu’il envoie. Un message chiffré à l’aide d’une clé privée peut être déchiffré par tout le monde grâce à la clé publique correspondante prouvant l’authenticité du message, un message chiffré avec une clé publique ne peut être déchiffré qu’avec la clé privée assurant la confidentialité.

En pratique, le chiffrement asymétrique est assez couteux en énergie et en temps de calcul, on préfère donc la cryptographique symétrique, à l’aide d’une clé partagée entre les utilisateurs créée à partir de leurs clés privées et publiques. Le processus de création de cette clé partagée assure que la confidentialité et l’authenticité sont conservées.

Cette création de clé partagée fonctionne très bien avec deux utilisateurs, c’est la méthode utilisée dans le monde entier pour sécuriser les échanges notamment sur Internet via HTTPS.

Mais dans le cas d’un échange chiffré de bout en bout sur une application de messagerie instantanée où trois utilisateurs ou plus souhaitent créer une telle clé, le processus ne fonctionne pas. Il faut alors avoir recours soit à du chiffrement asymétrique coûteux, soit à du chiffrement symétrique entre chaque paire d’utilisateurs ce qui multiplie les chiffrements, soit à la signature tour à tour de la clé par chaque utilisateur.

Il n’existe pas de protocole qui permette la création d’une clé partagée symétrique entre trois partis ou plus en un seul tour à partir de la clé privée d’un utilisateur et des clés publiques de tous les autres.

Deux partis : RSA et courbes elliptiques

L’échange de clés Diffie-Hellman permet de créer une clé partagée à partir d’une clé privée, de la clé publique de l’autre utilisateur et de paramètres définis au préalable. Cet échange repose sur la méthode de chiffrement RSA, qui utilise la congruence des nombres entiers et la difficulté algorithmique de la décomposition en facteurs premiers.

Le calcul de la clé partagée fonctionne de la manière suivante : soient $k_a$ la clé privée d’Alice et $k_b$ la clé privée de Bob deux entiers. En connaissant $p$ un nombre premier et $g$ un nombre entier définis à l’avance, Alice et Bob peuvent calculer leurs clés publiques, respectivement $k_A = g^{k_a}(\bmod{p})$ et $k_B = g^{k_b}(\bmod{p})$. Après s’être envoyé leurs clés publiques, Alice et Bob peuvent calculer leur clé partagée :

k_{ab} = {k_B}^{k_a}(\bmod{p}) = (g^{k_b})^{k_a}(\bmod{p}) = g^{ {k_a}{k_b} }(\bmod{p})

k_{ba} = {k_A}^{k_b}(\bmod{p}) = (g^{k_a})^{k_b}(\bmod{p}) = g^{ {k_a}{k_b} }(\bmod{p})

Depuis plusieurs années, le chiffrement asymétrique est plutôt réalisé grâce à la cryptographie sur les courbes elliptiques (Elliptic Curve Cryptography ou ECC) qui a progressivement remplacé le chiffrement RSA grâce ses clés bien plus courtes. Une courbe elliptique est un ensemble de points qui font partie de la courbe d’équation $y^2 = x^3+ax+b$, où $a$ et $b$ sont les paramètres de la courbe elliptique. Ces courbes elliptiques possèdent une loi de composition interne semblable à une addition, ainsi qu’un produit scalaire comme loi de composition externe.

Dans la cryptographie sur les courbes elliptiques, les clés publiques sont des points de la courbe tandis que les clés privées sont des scalaires, c’est-à-dire des nombres entiers. Le calcul de clé partagée fonctionne ainsi : soient $k_a$ la clé privée d’Alice et $k_b$ la clé privée de Bob deux entiers. En connaissant $a$ et $b$ les paramètres de la courbe, ainsi que $G$ un point de cette courbe, Alice et Bob peuvent calculer leurs clés publiques, respectivement $k_A = {k_a}*G$ et $k_B = {k_b}*G$, où $*$ représente le produit scalaire entre un nombre entier un point de la courbe. Après s’être envoyé leurs clés publiques, Alice et Bob peuvent calculer leur clé partagée :

k_{ab} = k_a*k_B = k_ak_b*G

k_{ba} = k_b*k_A = k_ak_b*G

En pratique, les courbes utilisées sont des courbes elliptiques sur corps finis, car les calculs y sont réalisés modulo $p$ un nombre premier pour des raisons similaire au chiffrement RSA. Le nombre premier $p$ est un paramètre de la courbe sur corps finis comme $a$ et $b$.

Implémentation

Une démonstration est disponible dans demo.py, qui va choisir des clés privées aléatoires pour Alice, Bob et Charlie et calculer les clés partagées du point de vue de chacun d’entre eux avec la cryptographie RSA et sur les courbes elliptiques. Les calculs sur les courbes elliptiques sont fait en important classes.py, qui peut aussi être exécuté seul.

Les options sont disponibles avec python3 demo.py --help :

usage: demo.py [-h] [-v] [-p PRIME] [-g NUM] [-a NUM] [-b NUM] [-m NUM] [-c] [-d] [-P]

options:
  -h, --help            show this help message and exit
  -v, --version         show program's version number and exit
  -p PRIME, --prime PRIME
                        prime number used for modulo in RSA and Finite fields ECC
  -g NUM, --generator NUM
                        number used for Diffie-Hellman exchange
  -a NUM                coefficient a of the Weierstrass form
  -b NUM                coefficient b of the Weierstrass form
  -m NUM, --max-key NUM
                        maximum value for random private key generation
  -c, --continuous      run the regular Elliptic Curve take quite a long
  -d, --debug           print additionnal information
  -P, --plot            plot graph with curve and points

Par défault, l’exécution ne prend pas en compte le calcul sur courbe elliptique sans corps finis. Pour cela, il faut utiliser l’option --continuous et il est conseillé de réduire la valeur maximale possible des clés privées à l’aide de --max-key pour diminuer considérablement le temps d’exécution.

Le but de cette implémentation est de montrer de manière non rigoureuse que RSA et les courbes elliptiques ne permettent pas de créer des clés identiques au delà de deux partis.

Trois partis : cryptographie à base de couplage

La cryptographie à base de couplage (Pairing Based Cryptography ou PBC) utilise des courbes elliptiques ainsi qu’une fonction entre ces courbes appelée couplage $e:G_1\times G_2\to G_T,\;(P,Q)\mapsto e(P,Q)$. On souhaite que le couplage soit bilinéaire, c’est-à-dire $e(P+R,Q)=e(P,Q)+e(R,Q)$ et $e(P,Q+S)=e(P,Q)+e(P,S)$ et non dégénératif $e\ne1$. Un couplage est dit symétrique lorsque $G_1=G_2$, alors $e:G^2\to G_T$.

Le calcul de la clé partagée fonctionne de la manière suivante : soient $k_a$ la clé privée d’Alice, $k_b$ la clé privée de Bob et $k_c$ la clé privée de Charlie trois entiers. En connaissant $e$ un couplage symmétrique et $P$ un point de la courbe $G$ définis à l’avance, Alice, Bob et Charlie peuvent calculer leurs clés publiques, respectivement $k_A = k_a*P$, $k_B = k_b*P$ et $k_C = k_c*P$. Après s’être envoyé leurs clés publiques, Alice et Bob peuvent calculer leur clé partagée :

k_{abc} = e(k_B, k_C)^{k_a} = e(k_b*P, k_c*P)^{k_a} = e(P, P)^{k_ak_bk_c}

k_{bca} = e(k_C, k_A)^{k_b} = e(k_c*P, k_a*P)^{k_b} = e(P, P)^{k_ak_bk_c}

k_{cab} = e(k_A, k_B)^{k_c} = e(k_a*P, k_b*P)^{k_c} = e(P, P)^{k_ak_bk_c}

Si le couplage n’est pas symétrique, alors Alice, Bob et Charlie doivent se mettre d’accord sur deux points $P_1\in G_1$ et $P_2\in G_2$. Ils calculent et divulguent alors deux clés publiques chacun, une sur chaque courbe. Cela ne change pas le calcul de la clé partagée.

Pour construire un couplage à partir d’une courbe elliptique sur corps fini, il existe différentes méthodes.

Note : section incomplète

Couplage Weil

Soit $q$ un nombre premier tel que $q\equiv 3\bmod 4$, alors $-1$ est un résidu dans $\mathbb F_q$ le corps fini de taille $q$. Soit $E:y^2 = x^3+x$, alors le cardinal de $E(\mathbb F_q)$ est $\#E(\mathbb F_q)=q+1$, on a également $\#E({\mathbb F_q}^2)=(q+1)^2$. Soit $r$ le plus grand nombre premier diviseur de $q+1$, alors $E(\mathbb F_q)$ contient un sous-groupe $G$ cyclique d’ordre $r$ et $E({\mathbb F_q}^2)$ contient un groupe isomorphique à $\mathbb Z_r\times \mathbb Z_r$.

$\phi:E(\mathbb F_q)\to E({\mathbb F_q}^2),\;(x,y)\mapsto (-x,iy)$

Couplage Tate

Soit $E$ une courbe elliptique sur $K={\mathbb F_q}^k$ un corps fini d’ordre $r$ premier avec $char(K)$ la caractéristique de $K$. Alors $K$ contient les racines r-ièmes de l’unité. Ou plus simplement, $r$ divise $ord(K)-1$.

$e:E[r]\cap E(K)\times E(K)/rE(K) \to K^*/K^{*r},\;(P,Q)\mapsto f_P(A_Q)$

$e(P,Q)=f_P(A_Q)^{(q^k+1)/r}$ où $P\in E/\mathbb F$ est d’ordre $r$ et $Q\in E/{\mathbb F_q}^k$

Couplage optimal Ate

$`N`$ partis : généralisation

Pour généraliser le cas à trois partis avec $N$ utilisateurs, sans restriction sur $N$, avec la cryptographie à base de couplage il faudrait trouver un couplage avec pour ensemble de départ $N$ courbes elliptiques $e:G_1\times ...\times G_N\to G_T,\;(P_1,...,P_N)\mapsto e(P_1,...,P_N)$. Il faut toujours s’assurer de la bilinéarité de $e$. Si $e$ est symétrique, on pourra noter $e:G^N\to G_T$. Si de tels couplages sont possibles, il n’existe a priori pas de méthode permettant d’en trouver à partir seulement des courbes $G_1$ à $G_N$.

Dans le cas d’usage d’une application de messagerie instantanée, cette méthode implique que le couplage nécessaire à l’échange de la clé partagée doit être recalculé à chaque fois qu’un utilisateur entre ou sort de la conversation. Alternativement, un ensemble de couplages peut être prédéfini pour $N$ allant de 3 à une valeur maximale, qui serait le nombre maximal d’utilisateurs dans un groupe.

Que ce soit grâce à la cryptographie à base de couplage ou autrement, la méthode de calcul de clé partagée doit encore être trouvée, prouvée et implémentée pour la généralisation à $N$ partis.

Échange de clé Diffie-Hellman en plusieurs tours

En l’absence de généralisation à $N$ partis d’une méthode de création de clé partagée en un seul tour, il est tentant d’utiliser un modèle d’échange de clé standard à base de Diffie-Hellman sur des courbes elliptiques. Plusieurs modèles de création de clé partagée avec leurs avantages et leurs inconvénients sont listés ci-dessous. Ces modèles supposent que les utilisateurs connaissent au préalable les clés publiques de chacun.

clé partagée aléatoire créé par un utilisateur maître
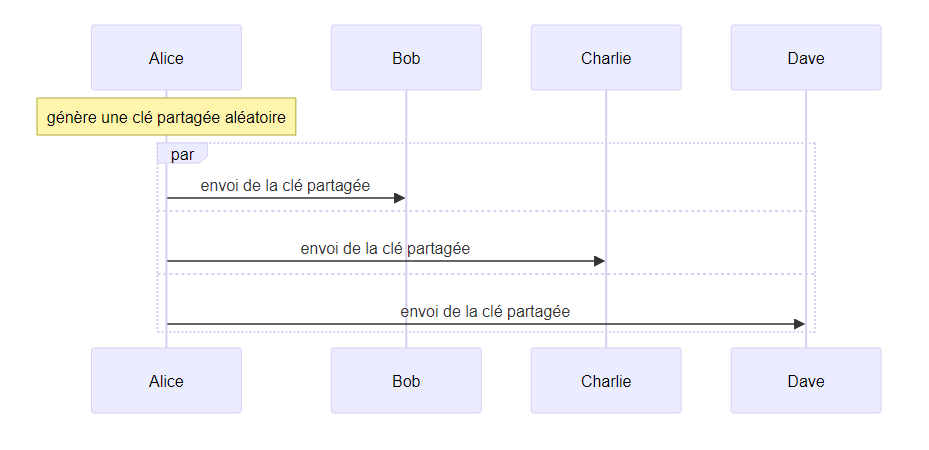
- point négatif : la clé partagée est envoyée, il suffirait de casser le chiffrement d’un message pour compromettre toute la sécurité
- point négatif : la clé partagée est envoyée plusieurs fois avec différents chiffrements, ce qui peut faciliter une attaque
- point négatif : la clé partagée est créée par un seul utilisateur, auquel les autres doivent faire confiance et dont la génération de nombre aléatoires pourrait être défaillante
- point positif : la procédure ne prend qu’un seul tour, les messages sont envoyés en parallèle
- point positif : le faible nombre de messages, $n-1$ pour $n$ utilisateurs
- point positif : la procédure n’a pas besoin d’être réalisée de nouveau lors de l’ajout d’un nouvel utilisateur
- point positif : l’ajout d’un nouvel utilisateur peut être fait de manière synchrone par un seul utilisateur
clé partagée aléatoire créée conjointement par tous les utilisateurs
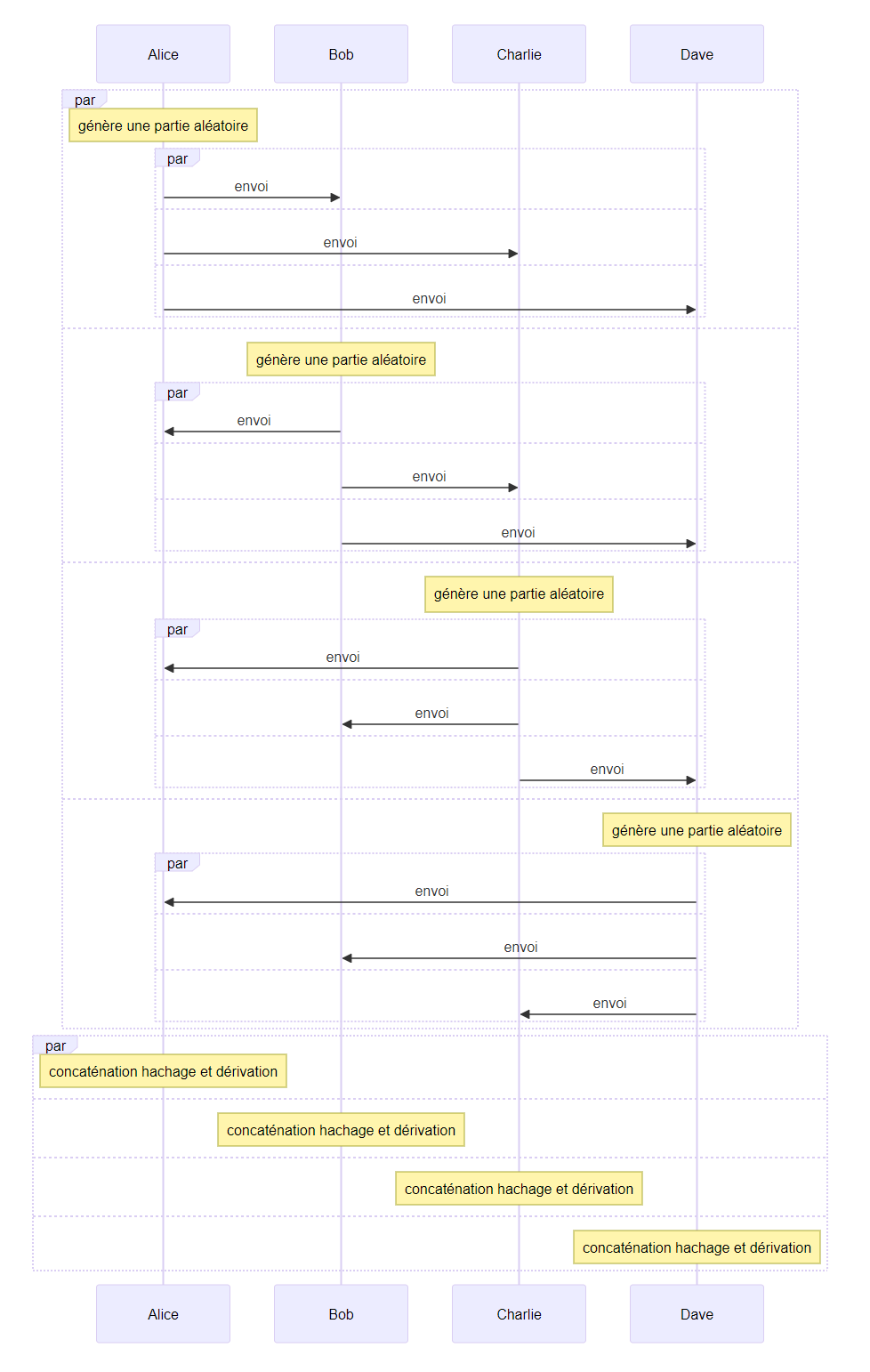
- point négatif : la clé partagée est envoyée, il suffirait de casser le chiffrement de quelques messages pour compromettre toute la sécurité
- point négatif : le très grand nombre de messages, $n(n-1)$ pour $n$ utilisateurs
- point négatif : l’ajout d’un nouvel utilisateur doit être fait de manière synchrone par tous les utilisateurs
- point positif : la clé partagée est créée à partir de tous les utilisateurs
- point positif : la procédure ne prend qu’un seul tour, les messages sont envoyés en parallèle
- point positif : la procédure n’a pas besoin d’être réalisée de nouveau lors de l’ajout d’un nouvel utilisateur
signature successive de la clé partagée coordonnée par un utilisateur maître
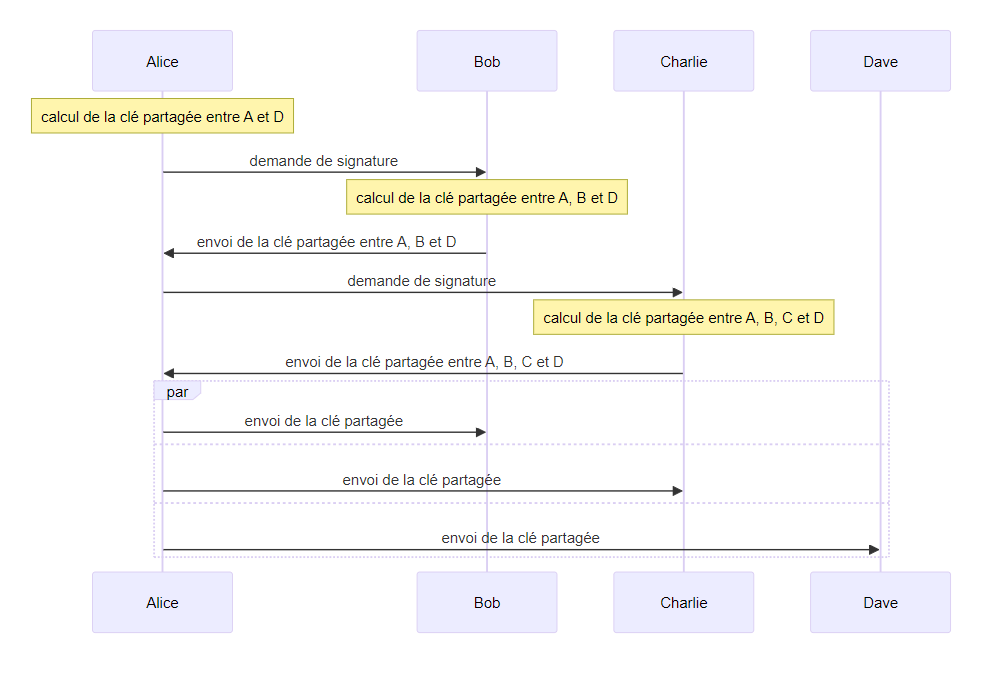
- point négatif : la clé partagée est envoyée, il suffirait de casser le chiffrement d’un message pour compromettre toute la sécurité
- point négatif : le grand nombre de messages, $3n-5$ pour $n$ utilisateurs
- point négatif : certains utilisateurs connaissent des clés partagées desquelles ils ne font pas partie, exemple B connait la clé entre A et D
- point négatif : l’ajout d’un nouvel utilisateur doit être fait de manière synchrone par tous les utilisateurs
- point positif : la clé partagée est créée à partir de tous les utilisateurs
échanges de clés Diffie-Hellman circulaires
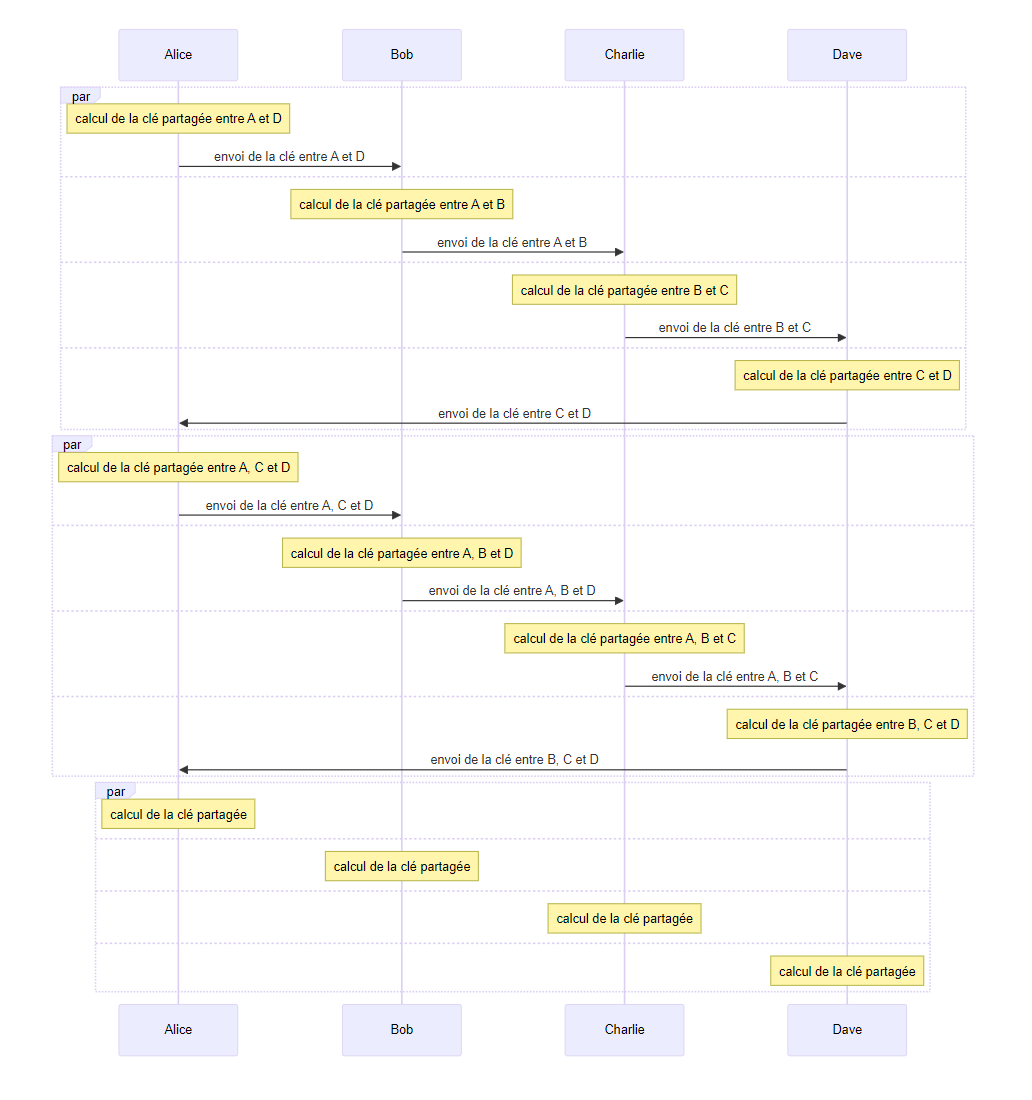
- point négatif : de nombreux utilisateurs connaissent des clés partagées desquelles ils ne font pas partie, exemple B connait la clé entre A et D
- point négatif : le très grand nombre de messages, $n(n-2)$ pour $n$ utilisateurs
- point négatif : l’ajout d’un nouvel utilisateur doit être fait de manière synchrone par tous les utilisateurs
- point positif : la clé partagée est créée à partir de tous les utilisateurs
- point positif : la clé partagée finale n’est pas envoyée

Ces quatre solutions, la clé partagée aléatoire créé par un utilisateur maître, la clé partagée aléatoire créée conjointement par tous les utilisateurs, la signature successive de la clé partagée coordonnée par un utilisateur maître et les échanges de clés Diffie-Hellman circulaires peuvent probablement utiliser la cryptographie à base de couplage afin de réduire le nombre d’échanges nécessaires.

Cependant, tant qu’il y aura strictement plus de trois utilisateurs et que la cryptographie à base de couplage ou autre cryptographie ne permet pas de généralisation à $N$ partis, il y aura nécessairement plusieurs tours pour réaliser l’échange de clé, ce qui empêche certains cas d’usages tels que le Double Ratchet du protocole Signal.

Liens utiles

Implémentation de cryptographie sur les courbes elliptiques

Introduction à la cryptographie à base de couplage

Articles scientifiques

Software Development Kit

Adrian Bonnet • Relex12.github.io • Hosted on GitHub Pages • Powered by Jekyll